
神经网络是深度学习的基础,上节提到由LR能够联系到神经网络,本节就对神经网络和BP算法进行一个回顾和总结。
1.由LR到神经网络
前面在逻辑回归的文章末尾提到,当样本是线性不可分时,需要对样本数据进行转换,转换过后在进行分类,那么转换的这个步骤就成为特征的提取的过程,结构如图所示:
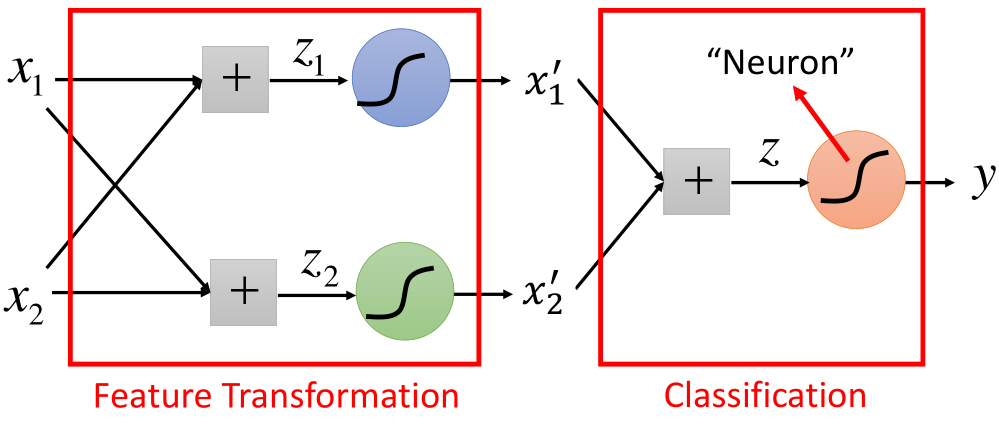
如上图所示,图中的结构每进行一次转换的结构,就称为一个神经元,还可以有如下这样的结构:
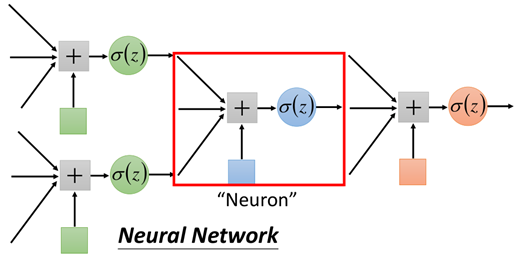
同样,一个红色的框起来的部分称之为神经元,神经元不同的连接方式,会产生不同的模型,模型的参数都包含在神经元的内部。
值得一提的是,在前面LR中说,当数据线性不可分时,需要我们自己去找特征转换的方程,使得样本变成线性可分的,然后再使用LR进行分类;
然而在神经网络中,不需要我们去找转换的方程,参数包含在网络中,一起进行训练,但这时需要我们自己去设计网络的结构,来找出合适的模型(参数),从而得到好的结果。
2.全连接神经网络
网络/模型结构
按照机器学习的三步走理论,首先我们需要确定模型,就是模型长什么样子,这里介绍一种全连接神经网络。
上面说到神经网络神经元之间的连接方式,决定了神经网络各种各样的模型和结构,下面说一种最常见的神经网络结构——全连接神经网络:
顾名思义,全连接神经网络就是每个神经元都相互连接,首先通过一个例子看一下一个结构的传播过程:

左边为输入(1,-1),每个箭头指向为权重参数w,绿色的方框为偏差b,首先进行线性相加,然后经过sigmoid方程,得到输出后,将该输出作为下一次传播的输入,继续向前:

那么上面的这个过程,利用向量的形式表示为:
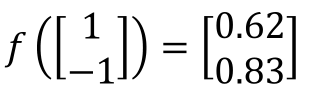
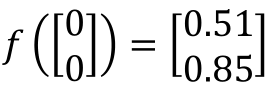
将第一节的图中方框的神经元“neuron”用“○”代替,那么全连接神经网络的结构如下:

上面就是一个较为完整全连接神经网络结构,最左侧为输入,称之为输入层,最右侧为输出,称之为输出层,在输入出与输出层之间的结构称之为隐藏层;
值得注意的是,在神经网络中,左侧的靠近输入层的称之为“后”,右侧靠近输出层的结构称之为“前”。因此上面那个例子的传播方式也称之为前向传播。
那么上面的示例的前向传播过程,我们用向量的形式来表示,这里只看第一层的过程:

第一层中的四个权重,利用向量的形式表示为:
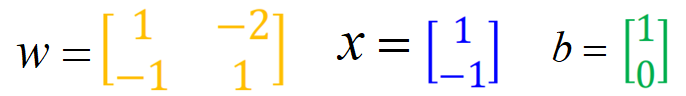
然后再经过sigmoid函数:
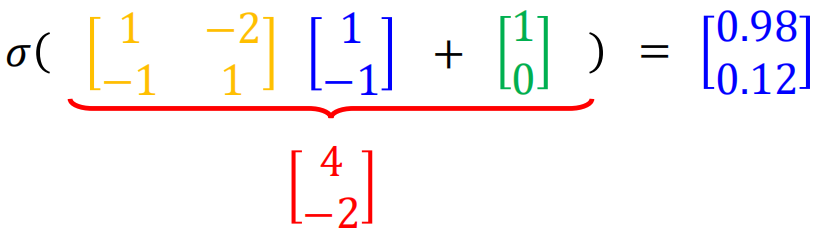
可以看到每一个神经元其实就是一个LR单元,总的来说,神经网络前向传播的向量形式即为:
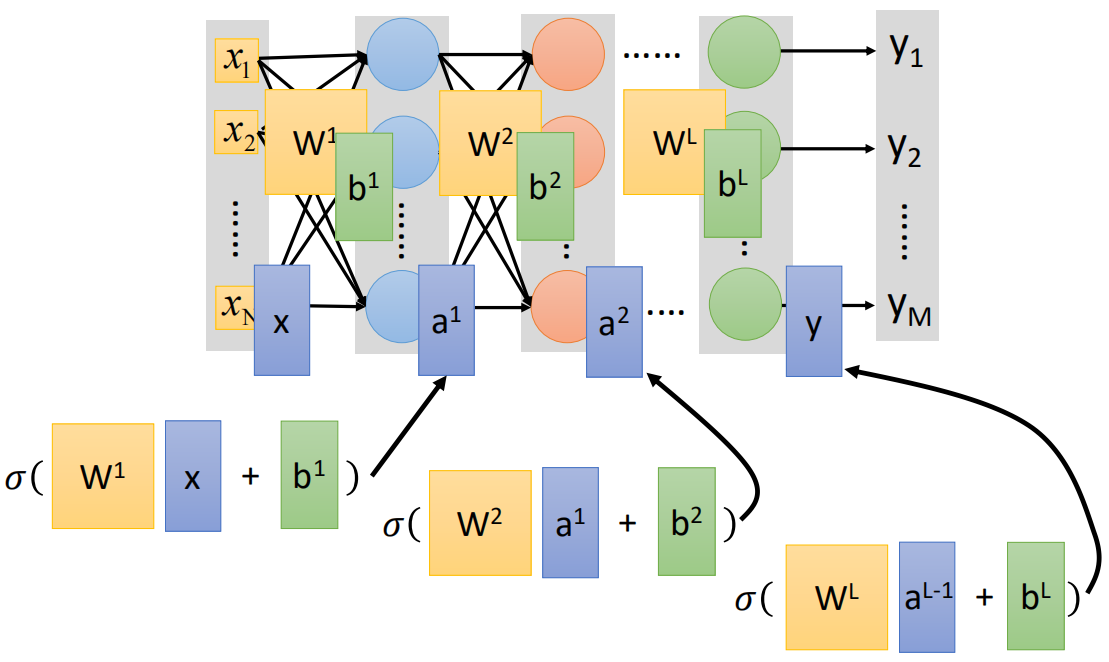

每一层的输出即是下一层的输入,直到最后的输出层。上面就是神经网络正向传播的过程。
在多分类问题中,通常最后一层的输出层为用于多分类的Softmax函数。

3.模型的训练以及BP算法
网络的结构需要我们初始给定,即网络的层数、每个网络所含有的神经元个数,确定了网络模型的结构也就确定了参数的数量,那么接下来就是找出最好的一组参数,也就是模型的训练。
根据在LR中我们计算损失的方式,在神经网络中,同样我们期望真实值与预测值越接近越好,因此在此同样采用交叉熵作为损失函数,不同的是,在LR中交叉熵的推导来自于最大似然估计的推导,而这里直接使用交叉熵公式,期望样本的真实分布与预测的分布越接近越好,即:
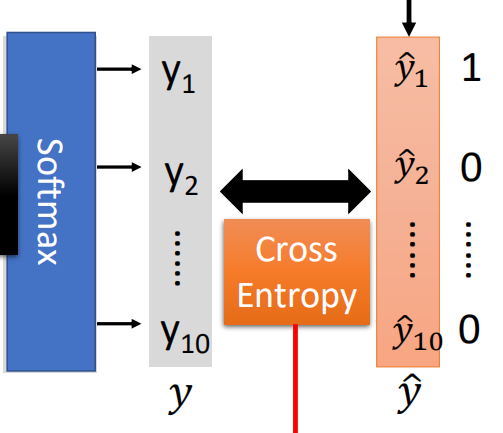
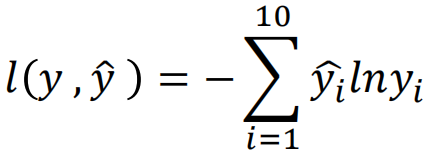
这里假设多分类的类别为10类,那么需要计算每一个维度之间的交叉熵,然后加和得到一个样本的交叉熵,对于多个样本,将所有样本再次相加即为交叉熵损失函数:
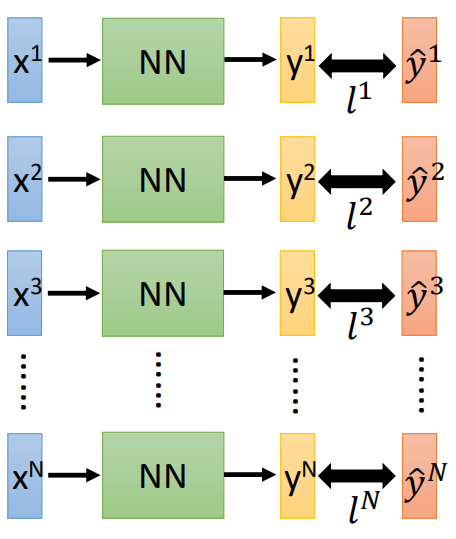
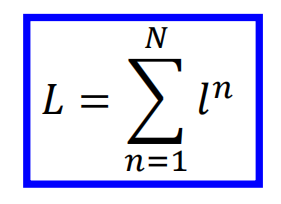
然后就是利用梯度下降进行求解,其梯度为:
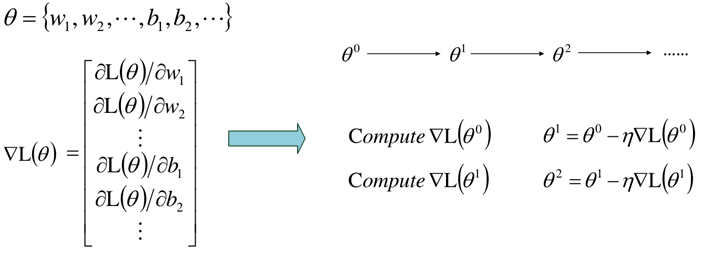
这种前向传播的梯度下降训练方式跟之前的一致,但是,当网络过于复杂时,参数的数量也过于庞大,这样可能目标损失函数过于复杂,直接求导难度较大,因此为更有效地计算梯度,通常采用BP反向传播算法。
BP算法原理
神经网络的损失函数为L(θ),那么损失函数对参数的导数为:
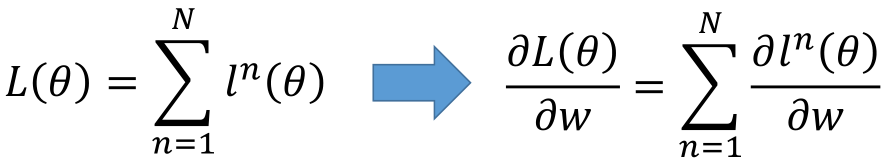
首先拿出一个神经元来看:
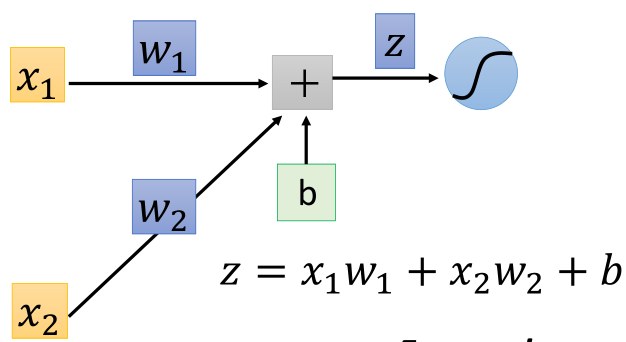
根据链式求导法则:

这里可以看到,导数的第一部分,即z对w的导数即为w所对应的输入x,比如下面这个例子:
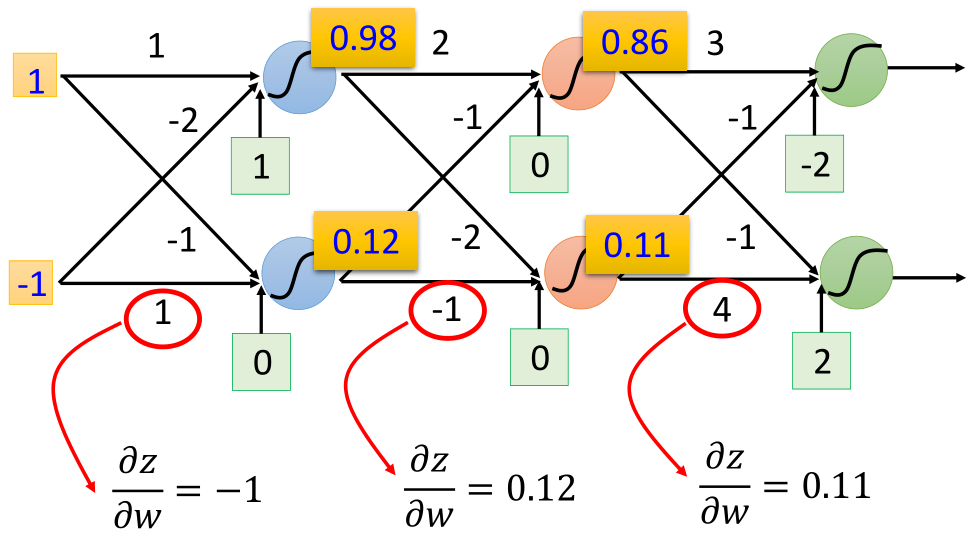
接下来看链式求导所得导数的后半部分,假设这一个神经元的输出为a,那么进一步利用链式求导法则:
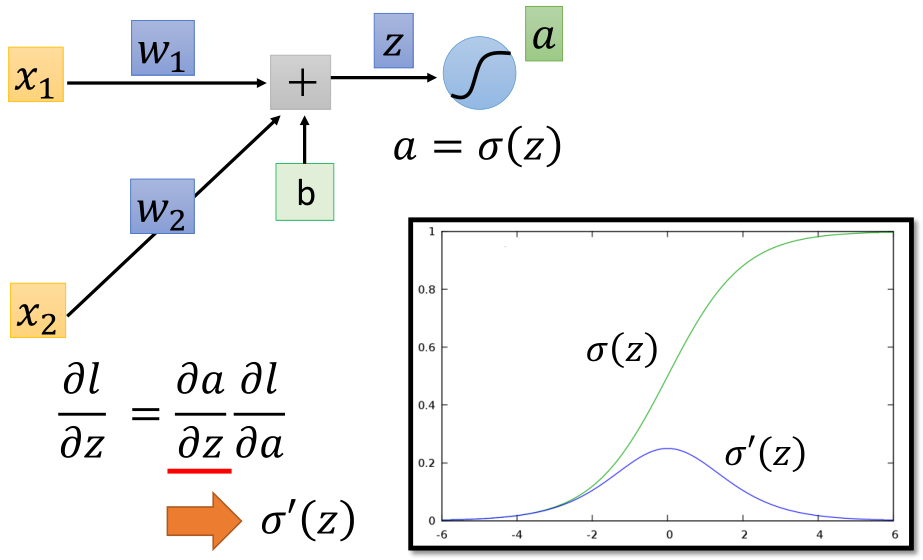
导数的前半部分导数即为sigmoid函数的导数σ'(z),然后就是后半部分,a为该层的输出,同时也是下一层网络的输入,与l有关,那么继续到下一层:

a作为后面网络的输入,影响到下一层网络的每一个输出,假设下一层有两个神经元,那么a经过线性加权,分别得到z'和z'',那么根据链式求导法则:

两个部分,每一部分的前半部分为输入a对应的连接的权重w,即:
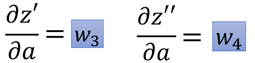 .
.
那么有:
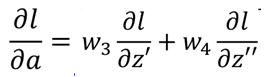
那么回到第一步的l对z的求导结果:
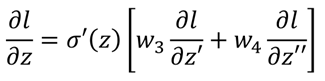
如果到这一步就到达了输出层,那么这里就可以知道l分别对z'和z''的导数了,因为:
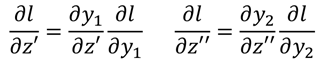
然后就可以求得l对w的导数了。
如果这一步没有到达输出层,那么就继续进入下一层:
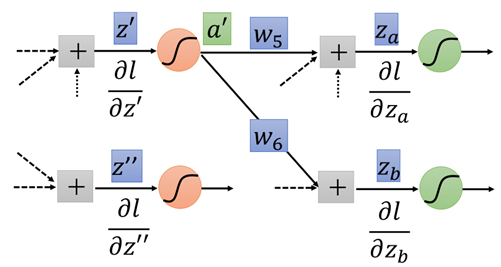
继续重复上述步骤即可,直到到达输出层。
那么从上面的过程来看,我们在计算l对z的导数,需要一步一步递归地向后计算,直到传播到输出层,然后求输出层y对前一层的导数,再一步一步向后(输入层)传,最终得到l对w的导数,即梯度,就可以利用梯度下降进行迭代了。
因此上面的过程就是一个反向传播的过程,如图所示:
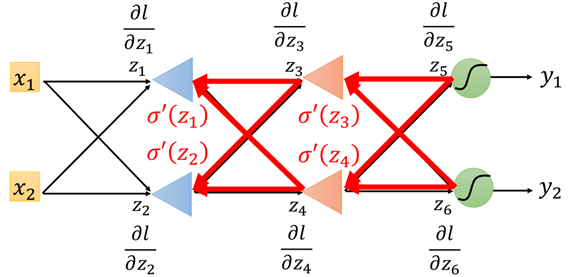
根据上面的过程,在前向传播中求链式求导结果中,每一项的第一部分,这一部分较容易直接求导得出的,反向传播求得每一项的第二部分,这一部分需要不断地递归求得,如图所示:

4.利用Keras实现深度学习
下面就通过一个实例,来实现神经网络(深度学习),并说明每一步的作用。
首先数据集来源与MNIST的手写数字辨识数据集,数据是手写的0~9的图片数据,首先导入所需要的的库,并从sklearn读取数据集并对数据作处理:
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
import numpy as np
from keras import Sequential
from keras.layers import Dense
from keras.layers import Activation
import matplotlib.pyplot as plt
import matplotlib as mpl
data_x, data_y = fetch_openml('mnist_784', version=1, return_X_y=True)
# 将大于0的置为1,只要0和1的图片数据
data_x[data_x > 0] = 1
data_x = np.mat(data_x)
one_hot = OneHotEncoder()
data_y = one_hot.fit_transform(np.array(data_y).reshape(data_y.shape[0], 1)).toarray()
train_x, test_x, train_y, test_y = train_test_split(data_x, data_y)
先来看一下数据长什么样子:
data_x[:10] #### matrix([[0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.], ..., [0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.], [0., 0., 0., ..., 0., 0., 0.]]) data_y[:10] #### array([[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], [1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0., 0., 0., 0., 1.], [0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 1., 0., 0., 0., 0., 0.]])
X是28*28共784维的稀疏矩阵,Y经过独热编码后每一个数据是一个10维的数据,我们画一下任意一张来看一下:
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap=mpl.cm.binary, interpolation='nearest')
plt.axis("off")
one_digit = data_x[10000]
plot_digit(one_digit)
数据准备好后,就到了建模的阶段,利用keras神经网络框架建模:
首先是网络结构,需要我们自己定一个网络结构,包括网络层数、每个层数的神经元个数,这里输入为28*28维,因此输入层为784维,输出为10维,输出层结构10。中间层我们暂定为500,那么网络结构如图所示:

然后就是利用keras对上面网络进行建模的过程:

这样模型就建好了,接下来就是对模型进行编译,这里与之前的不太一样,之前直接定义好模型和参数就可以fit了:
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
可选的optimizer就是之前的梯度下降那一节介绍的参数优化方法,详见:https://www.cnblogs.com/501731wyb/p/15322391.html
可选的loss也有很多,可见官方文档:https://keras.io/zh/losses/。
接下来利用数据进行训练了:
model.fit(train_x, train_y, batch_size=300, epochs=20)
这里batch_size就是训练中采用一批数据进行训练,选完一批继续下一批,直到所有数据完成一次,成为1个epoch。

然后查看训练结果,以及在测试集上的表现:
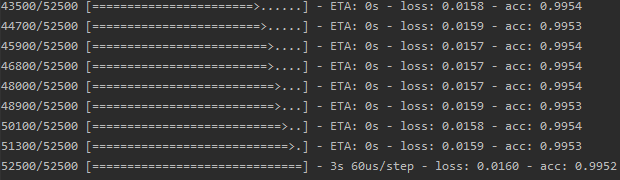
score = model.evaluate(test_x, test_y)
print('total loss on testing data', score[0])
print('accuracy on testing data', score[1])
32/17500 [..............................] - ETA: 17s
1120/17500 [>.............................] - ETA: 1s
2272/17500 [==>...........................] - ETA: 0s
3648/17500 [=====>........................] - ETA: 0s
5216/17500 [=======>......................] - ETA: 0s
6720/17500 [==========>...................] - ETA: 0s
8224/17500 [=============>................] - ETA: 0s
9888/17500 [===============>..............] - ETA: 0s
11648/17500 [==================>...........] - ETA: 0s
13376/17500 [=====================>........] - ETA: 0s
15072/17500 [========================>.....] - ETA: 0s
16864/17500 [===========================>..] - ETA: 0s
17500/17500 [==============================] - 1s 35us/step
total loss on testing data 0.116816398623446
accuracy on testing data 0.9730285714285715
可以看到,在训练集上有99.53左右的精确度,在测试集上有97.3%的准确率,测试数据共有17500张图片,其中错误分类的又472张,我们找出这472张:
error_idx = [] for i in range(len(test_x)): predict_array = model.predict(test_x[i]) true_array = test_y[i] predict_result = np.argmax(predict_array) true_idx = np.argwhere(true_array == 1)[0][0] if true_idx != predict_result: error_idx.append(i)
然后看一下这些分错的数据,先写一个批量画图的函数:
def plot_digits(instances, image_per_row=10, **options):
size = 28
image_per_row = min(len(instances), image_per_row)
images = [instance.reshape(28, 28) for instance in instances]
n_rows = (len(instances) - 1)//image_per_row + 1
row_images = []
n_empty = n_rows * image_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row*image_per_row:(row+1)*image_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap=mpl.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(9, 9))
然后画出来一部分数据,看下为啥会分错:
example_images = [] for idx in error_idx[:30]: example_images.append(test_x[idx]) plot_digits(example_images, image_per_row=10)

从这些图片上可以看到,这些分错的数据中一大部分还是很难区分的,比如第二排第一张,肉眼都是比较难区分的。
这是可能是因为对于特征的提取还是不够充分,导致错误分类,需要进一步调整模型,下一节主要说一下深度学习中的一些优化策略。
神经网络到这里初步介绍完毕了,主要介绍了全连接神经网络和BP算法,并利用keras框架进行了实现,完成了深度学习的"Hello World"。
内容主要来源于李宏毅老师的课程,由于看的时间比较久了,这里再回顾一下,事情比较多,总算完结了,下一节主要总结一下常用的损失函数及特性,以及在深度学习中一些模型优化和调整策略。
